Research
Scientific Interests
My research interests lie in uncovering the mechanisms behind complex
phenomena occurring in nature, society and technology;
and in the mathematical modeling of biological and technological systems using first
principles.
I study both fundamental problems in dynamical
systems and network theory;
and applications in complex systems in biology, biomedicine and neuroscience.
Research methods include:
- Methods from applied math and theoretical physics
- Dynamical systems and bifurcation theory
- Network and graph theory
- Numerical methods, simulations, high performance computing
- Collaboration with experimentalists
Research topics
Research topics include:
- Dynamical systems theory and network science
- Adaptive dynamic transport networks
- Synchronization dynamics in complex networks
- Synchronization theory and mathematical
neuroscience
- Chimera states and symmetry breaking synchronization patterns
- Synchronization in co-evolutionary adaptive networks
- Dynamics and synchronization in neuronal neurons
- Oscillations and resonance in complex networks
- Dynamics, networks and self-organization in bio-medicine and biology
- Complex networks, time series and tipping points
Research Highlights
The synchronization of coupled oscillators is a striking manifestation of self-organization that nature employs to orchestrate essential processes of life, such as the beating of the heart. While it was long thought that synchrony or disorder were mutually exclusive steady states for a network of identical oscillators, numerous theoretical studies over the last 10 years revealed the intriguing possibility of `chimera states', in which the symmetry of the oscillator population is broken into a synchronous and an asynchronous part. Particularly, numerous analytical studies, involving different network topologies, and various sources of random perturbations establish chimeras as a robust theoretical concept and suggest that they exist in complex systems in nature. Yet, a striking lack of empirical evidence raises the question of whether chimeras are indeed characteristic to natural systems. This calls for a palpable realization of chimera states without any fine-tuning, from which physical mechanisms underlying their emergence can be uncovered. Here, we devise a simple experiment with mechanical oscillators coupled in a hierarchical network to show that chimeras emerge naturally from a competition between two antagonistic synchronization patterns. We identify a wide spectrum of complex states, encompassing and extending the set of previously described chimeras. Our mathematical model shows that the self-organization observed in our experiments is controlled by elementary dynamical equations from mechanics that are ubiquitous in many natural and technological systems. The symmetry breaking mechanism revealed by our experiments may thus be prevalent in systems exhibiting collective behaviour, such as power grids, opto-mechanical crystals or cells communicating via quorum sensing in microbial populations.
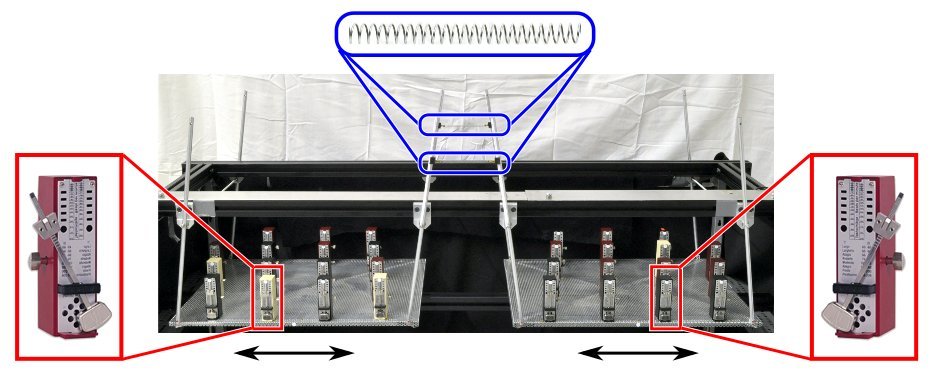 Experimental setup with 16 metronomes on two swings with spring coupling.
Experimental setup with 16 metronomes on two swings with spring coupling.
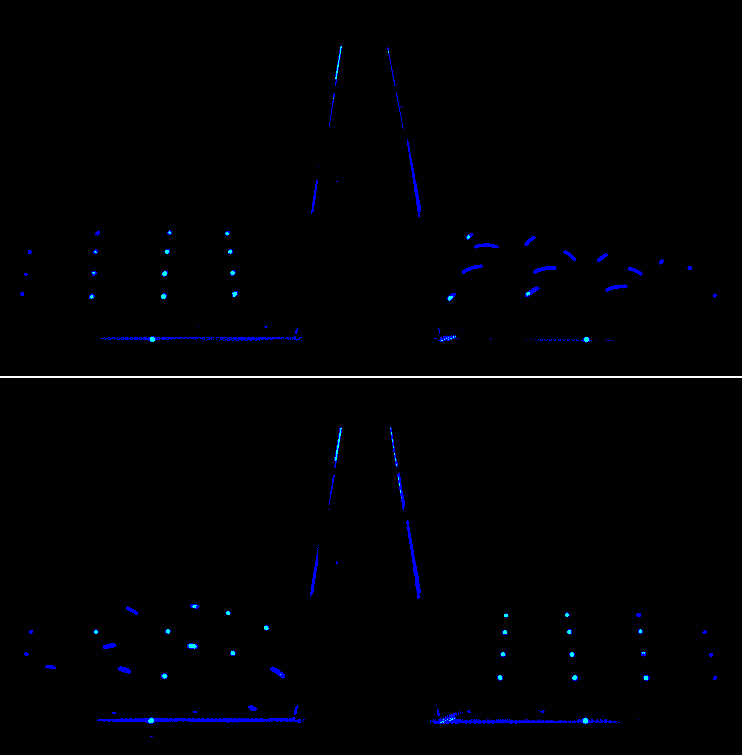 The motion of metronome pendula, fluorescently marked, is highlighted with UV light, thus revealing synchrony and desynchrony in the left or right population.
The motion of metronome pendula, fluorescently marked, is highlighted with UV light, thus revealing synchrony and desynchrony in the left or right population.
Selected publications
-
Chimera States in Mechanical Oscillator Networks.
Erik A. Martens, Shashi Thutupalli, Antoine Fourrière, Oskar Hallatschek.
Proc. Natl. Acad. Sci., Vol. 110 (26), p. 10563–10567 (2013), doi:10.1073/pnas.1302880110
- Intermittent chaotic chimeras for coupled rotators.
Simona Olmi, Erik A. Martens, Shashi Thutupalli, Alessandro Torcini.
Phys. Rev. E Rapid Communications, 92, 030901 (2015)
; arXiv:1507.07685
- Solvable Model of a Spiral Wave Chimeras.
Erik A. Martens, C. R. Laing and S. H. Strogatz.
Phys. Rev. Lett., Vol. 104, 044101 (2010); arXiv:0910.5389
-
Basins of Attraction for Chimera States.
Erik A. Martens, Mark Panaggio, Daniel M. Abrams.
New Journal of Physics, Fast Track Communication, 18:022002 (2016), Open Access; doi: 10.1088/1367-2630/18/2/022002; arXiv:1507.01457
-
Chimera States in Two Populations with Heterogeneous Phase-lag.
Erik A. Martens, Christian Bick and Mark J. Panaggio.
Chaos 26 (9), 094819 (2016); doi: 10.1063/1.4958930; arXiv:1606.0187
-
Chaos in Kuramoto Oscillator Networks.
Christian Bick, Mark J. Panaggio and Erik A. Martens.
Chaos (Editor's pick), 28, 071102 (2018), Fast Track; doi: 10.1063/1.5041444; arXiv:1802.05481
Selected publications
-
Cerebrospinal fluid influx drives acute ischemic tissue swelling.
H. Mestre, T. Du, A. M. Sweeney, G. Liu, A. J. Samson, W. Peng, K. Nygaard Mortensen, F. F. Stæger, P. A. R. Bork, L. Bashford, E. R. Toro, J. Tithof, D. H. Kelley, P. G. Hjorth, Erik A. Martens, R. I. Mehta, O. Solis, P. Blinder, D. Kleinfeld, H. Hirase, Y. Mori, M. Nedergaard
Science, Research Article (2020); doi:10.1126/science.aax7171;
-
Cyclic Structure Induced by Load Fluctuations in Adaptive Transportation Networks.
Erik A. Martens and Konstantin Klemm.
ECMI book subseries of Mathematics in Industry (2019); doi: 10.1007/978-3-030-27550-19; arXiv:1810.10049
-
Transitions from Trees to Cycles in Adaptive Flow Networks.
Erik A. Martens and Konstantin Klemm.
Frontiers in Physics, Vol. 5, Article 62, 2017, Open Access; arXiv:1711.00401
Selected publications
-
Understanding Synchrony Patterns in Biological and Neural Oscillator Networks through Mean-Field Reductions: A Review
Christian Bick, Carlo Laing, Marc Goodfellow and Erik A. Martens
Journal of Mathematical Neuroscience, 10(9) (2020); doi: 10.1186/s13408-020-00086-9;
arXiv:1902.05307
-
Exact Results for the Kuramoto Model with a Bimodal Frequency Distribution
Erik A. Martens, E. Barreto, S. H. Strogatz, E. Ott, P. So and T. Antonsen
Phys. Rev. E, Vol. 79, No.2 (2009); arXiv:0809.2129;
-
First-order Synchronization Transition in a Large Population of Strongly Coupled Relaxation Oscillators
Dumitru Călugăru, Jan Frederik Totz, Erik A. Martens and Harald Engel
Science Advances, 6(39):eabb2637 (2020), doi:10.1126/sciadv.abb2637; arXiv:1812.04727

