Publications & Talks
Publications
Citations on Google Scholar.
Find Supplementary Information for papers here.
Publications in Preparation (Under Review / Pre-prints)
-
Erik A. Martens, Mark Panaggio, Shashi Thutupalli
On the Origin of Chimera States in Mechanical Oscillator Networks
(In preparation);
> Abstract
Peer-Reviewed Publications (Published / in Press)
-
Rok Cestnik and Erik A. Martens
Integrability of a globally coupled complex Riccati array: quadratic integrate-and-fire neurons, phase oscillators and all in between
Phys. Rev. Lett. 132, 057201 (2024); doi:10.1103/PhysRevLett.132.057201; arXiv:2305.17683
PRL Editor's Suggestion. Read the PRL Viewpoint here.
> Abstract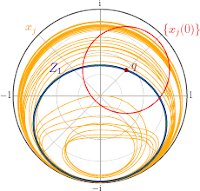 We present an exact dimensionality reduction for dynamics of an arbitrary array of globally coupled complex-valued Riccati equations. It generalizes the Watanabe-Strogatz theory [Integrability of a globally coupled oscillator array, Phys. Rev. Lett. 70, 2391 (1993).] for sinusoidally coupled phase oscillators and seamlessly includes quadratic integrate-and-fire neurons as the real-valued special case. This simple formulation reshapes our understanding of a broad class of coupled systems—including a particular class of phase-amplitude oscillators—which newly fall under the category of integrable systems. Precise and rigorous analysis of complex Riccati arrays is now within reach, paving a way to a deeper understanding of emergent behavior of collective dynamics in coupled systems.
We present an exact dimensionality reduction for dynamics of an arbitrary array of globally coupled complex-valued Riccati equations. It generalizes the Watanabe-Strogatz theory [Integrability of a globally coupled oscillator array, Phys. Rev. Lett. 70, 2391 (1993).] for sinusoidally coupled phase oscillators and seamlessly includes quadratic integrate-and-fire neurons as the real-valued special case. This simple formulation reshapes our understanding of a broad class of coupled systems—including a particular class of phase-amplitude oscillators—which newly fall under the category of integrable systems. Precise and rigorous analysis of complex Riccati arrays is now within reach, paving a way to a deeper understanding of emergent behavior of collective dynamics in coupled systems.
-
Konstantin Klemm and Erik A. Martens
Bifurcations in adaptive vascular networks: towards model calibration
Chaos 33:9, 093135 (2023); doi:10.1063/5.0160170; arXiv:2305.19401
> Abstract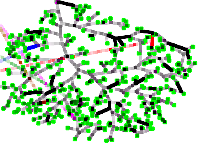 Transport networks are crucial for the functioning of natural and technological systems. We study a mathematical model of vascular network adaptation, where the network structure dynamically adjusts to changes in blood flow and pressure. The model is based on local feedback mechanisms that occur on different time scales in the mammalian vasculature. The cost exponent γ tunes the vessel growth in the adaptation rule, and we test the hypothesis that the cost exponent is γ = 1/2 for vascular systems [Hu and Cai, Phys. Rev. Lett., Vol. 111(13) (2013)1 ]. We first perform a bifurcation analysis for a simple triangular network motif with fluctuating demand, and then conduct numerical simulations on network topologies extracted from perivascular networks of rodent brains. We compare the model predictions with experimental data and find that γ is closer to 1 than to 1/2 for the model to be consistent with the data. Our study thus aims at addressing two questions: (i) Is a specific measured flow network consistent in terms of physical reality? (ii) Is the adaptive dynamic model consistent with measured network data? We conclude that the model can capture some aspects of vascular network formation and adaptation, but also suggest some limitations and directions for future research. Our findings contribute to a general understanding of the dynamics in adaptive transport networks, which is essential for studying mammalian vasculature and developing self-organizing piping systems.
Transport networks are crucial for the functioning of natural and technological systems. We study a mathematical model of vascular network adaptation, where the network structure dynamically adjusts to changes in blood flow and pressure. The model is based on local feedback mechanisms that occur on different time scales in the mammalian vasculature. The cost exponent γ tunes the vessel growth in the adaptation rule, and we test the hypothesis that the cost exponent is γ = 1/2 for vascular systems [Hu and Cai, Phys. Rev. Lett., Vol. 111(13) (2013)1 ]. We first perform a bifurcation analysis for a simple triangular network motif with fluctuating demand, and then conduct numerical simulations on network topologies extracted from perivascular networks of rodent brains. We compare the model predictions with experimental data and find that γ is closer to 1 than to 1/2 for the model to be consistent with the data. Our study thus aims at addressing two questions: (i) Is a specific measured flow network consistent in terms of physical reality? (ii) Is the adaptive dynamic model consistent with measured network data? We conclude that the model can capture some aspects of vascular network formation and adaptation, but also suggest some limitations and directions for future research. Our findings contribute to a general understanding of the dynamics in adaptive transport networks, which is essential for studying mammalian vasculature and developing self-organizing piping systems.
-
Benjamin Jütter and Erik A. Martens
Complex dynamics in adaptive networks of phase oscillators
Chaos, 33, 053106 (2023); doi:10.1063/5.0133190; arXiv:2209.10514
> Abstract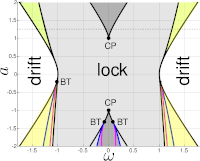 Networks of coupled dynamical units give rise to collective dynamics such as the synchronization of oscillators or neurons in the brain. The ability of the network to adapt coupling strengths between units in accordance with their activity arises naturally in a variety of contexts, including neural plasticity in the brain, and adds an additional layer of complexity: the dynamics on the nodes influence the dynamics of the network and vice versa. We study a minimal model of Kuramoto phase oscillators including a general adaptive learning rule with three parameters (strength of adaptivity, adaptivity offset, adaptivity shift), mimicking learning paradigms based on spike-time-dependent plasticity. Importantly, the strength of adaptivity allows to tune the system away from the limit of the classical Kuramoto model, corresponding to stationary coupling strengths and no adaptation and, thus, to systematically study the impact of adaptivity on the collective dynamics. We carry out a detailed bifurcation analysis for the minimal model consisting of N = 2 oscillators. The non-adaptive Kuramoto model exhibits very simple dynamic behavior, drift, or frequency-locking; but once the strength of adaptivity exceeds a critical threshold non-trivial bifurcation structures unravel: A symmetric adaptation rule results in multi-stability and bifurcation scenarios, and an asymmetric adaptation rule generates even more intriguing and rich dynamics, including a period-doubling cascade to chaos as well as oscillations displaying features of both librations and rotations simultaneously. Generally, adaptation improves the synchronizability of the oscillators. Finally, we also numerically investigate a larger system consisting of N = 50 oscillators and compare the resulting dynamics with the case of N = 2 oscillators.
Networks of coupled dynamical units give rise to collective dynamics such as the synchronization of oscillators or neurons in the brain. The ability of the network to adapt coupling strengths between units in accordance with their activity arises naturally in a variety of contexts, including neural plasticity in the brain, and adds an additional layer of complexity: the dynamics on the nodes influence the dynamics of the network and vice versa. We study a minimal model of Kuramoto phase oscillators including a general adaptive learning rule with three parameters (strength of adaptivity, adaptivity offset, adaptivity shift), mimicking learning paradigms based on spike-time-dependent plasticity. Importantly, the strength of adaptivity allows to tune the system away from the limit of the classical Kuramoto model, corresponding to stationary coupling strengths and no adaptation and, thus, to systematically study the impact of adaptivity on the collective dynamics. We carry out a detailed bifurcation analysis for the minimal model consisting of N = 2 oscillators. The non-adaptive Kuramoto model exhibits very simple dynamic behavior, drift, or frequency-locking; but once the strength of adaptivity exceeds a critical threshold non-trivial bifurcation structures unravel: A symmetric adaptation rule results in multi-stability and bifurcation scenarios, and an asymmetric adaptation rule generates even more intriguing and rich dynamics, including a period-doubling cascade to chaos as well as oscillations displaying features of both librations and rotations simultaneously. Generally, adaptation improves the synchronizability of the oscillators. Finally, we also numerically investigate a larger system consisting of N = 50 oscillators and compare the resulting dynamics with the case of N = 2 oscillators.
-
André H. Erhard, Krasimira Tsaneva-Atanasova, Glenn Terje Lines and Erik A. Martens
Editorial: Dynamical Systems, PDEs and Networks for Biomedical Applications: Mathematical Modeling, Analysis and Simulations
Frontiers in Physics, Volume 10:1101756, (2023); doi:10.3389/fphy.2022.1101756;
> Abstract This Research Topic is focused on advanced methods in mathematical and computational modeling of biomedical phenomena using (experimental) data, theior analysis and numerical simulations that contribute to a significantly improved comprehension of these phenomena.
The main focus of this special isssue is three-fold: 1) modeling approaches using differential equations or networks describing the behavior of single cells, cell groups, tissue or organs. 2) The analysis of the dynamics and behavior of certain biomedical models improving the state-of-the-art understanding of certain phenomena like cardiovascular and neurological diseases and disorders. 3) Improved numerical methods to simulate and analyze complex biomedical models.
This Research Topic is focused on advanced methods in mathematical and computational modeling of biomedical phenomena using (experimental) data, theior analysis and numerical simulations that contribute to a significantly improved comprehension of these phenomena.
The main focus of this special isssue is three-fold: 1) modeling approaches using differential equations or networks describing the behavior of single cells, cell groups, tissue or organs. 2) The analysis of the dynamics and behavior of certain biomedical models improving the state-of-the-art understanding of certain phenomena like cardiovascular and neurological diseases and disorders. 3) Improved numerical methods to simulate and analyze complex biomedical models.
-
Marios Gkogkas, Benjamin Jüttner, Christian Kuehn, Erik A. Martens
Graphop Mean-field Limits and Synchronization for the Stochastic Kuramoto Model
Chaos 32:11 (2022); doi:10.1063/5.0094009; arXiv:2203.16839
> Abstract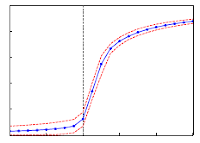 Models of coupled oscillator networks play an important role in describing collective synchronization dynamics in biological and technological systems. The Kuramoto model describes oscillator’s phase evolution and explains the transition from incoherent to coherent oscillations under simplifying assumptions, including all-to-all coupling with uniform strength. Real world networks, however, often display heterogeneous connectivity and coupling weights that influence the critical threshold for this transition. We formulate a general mean-field theory (Vlasov–Focker Planck equation) for stochastic Kuramoto-type phase oscillator models, valid for coupling graphs/networks with heterogeneous connectivity and coupling strengths, using graphop theory in the mean-field limit. Considering symmetric odd-valued coupling functions, we mathematically prove an exact formula for the critical threshold for the incoherence–coherence transition. We numerically test the predicted threshold using large finite-size representations of the network model. For a large class of graph models, we find that the numerical tests agree very well with the predicted threshold obtained from mean-field theory. However, the prediction is more difficult in practice for graph structures that are sufficiently sparse. Our findings open future research avenues toward a deeper understanding of mean-field theories for heterogeneous systems.
Models of coupled oscillator networks play an important role in describing collective synchronization dynamics in biological and technological systems. The Kuramoto model describes oscillator’s phase evolution and explains the transition from incoherent to coherent oscillations under simplifying assumptions, including all-to-all coupling with uniform strength. Real world networks, however, often display heterogeneous connectivity and coupling weights that influence the critical threshold for this transition. We formulate a general mean-field theory (Vlasov–Focker Planck equation) for stochastic Kuramoto-type phase oscillator models, valid for coupling graphs/networks with heterogeneous connectivity and coupling strengths, using graphop theory in the mean-field limit. Considering symmetric odd-valued coupling functions, we mathematically prove an exact formula for the critical threshold for the incoherence–coherence transition. We numerically test the predicted threshold using large finite-size representations of the network model. For a large class of graph models, we find that the numerical tests agree very well with the predicted threshold obtained from mean-field theory. However, the prediction is more difficult in practice for graph structures that are sufficiently sparse. Our findings open future research avenues toward a deeper understanding of mean-field theories for heterogeneous systems.
-
Douglas H. Kelley, Tomas Bohr, Poul G. Hjorth, Sebastian C. Holst, Sabina Hrabetová, Vesa Kiviniemi, Tuomas Lilius, Iben Lundgaard, Kent-Andre Mardal, Erik A. Martens, Yuki Mori, Valentin Nagerl, Charles Nicholson, Allen Tannenbaum, John H. Thomas, Jeffrey Tithof, Helene Benveniste, Jeffrey J. Iliff, and Maiken Nedergaard
The glymphatic system: Current understanding and modeling
iScience 25:9 (2022); doi:10.1016/j.isci.2022.104987;
> Abstract We review theoretical and numerical models of the glymphatic system, which circulates cerebrospinal fluid and interstitial fluid around the brain, facilitating solute transport. Models enable hypothesis development and predictions of transport, with clinical applications including drug delivery, stroke, cardiac arrest, and neurodegenerative disorders like Alzheimer's disease. We sort existing models into broad categories by anatomical function: perivascular flow, transport in brain parenchyma, interfaces to perivascular spaces, efflux routes, and links to neuronal activity. Needs and opportunities for future work are highlighted wherever possible; new models, expanded models, and novel experiments to inform models could all have tremendous value for advancing the field.
We review theoretical and numerical models of the glymphatic system, which circulates cerebrospinal fluid and interstitial fluid around the brain, facilitating solute transport. Models enable hypothesis development and predictions of transport, with clinical applications including drug delivery, stroke, cardiac arrest, and neurodegenerative disorders like Alzheimer's disease. We sort existing models into broad categories by anatomical function: perivascular flow, transport in brain parenchyma, interfaces to perivascular spaces, efflux routes, and links to neuronal activity. Needs and opportunities for future work are highlighted wherever possible; new models, expanded models, and novel experiments to inform models could all have tremendous value for advancing the field.
-
Oleksandr Burylko, Erik A. Martens, Christian Bick
Symmetry breaking yields chimeras in two small populations of Kuramoto-type oscillators
Chaos 32:9 (2022); doi:10.1063/5.0088465; arXiv:2202.10807
> Abstract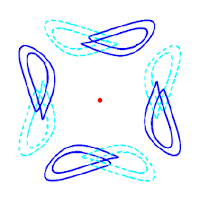 Despite their simplicity, networks of coupled phase oscillators can give rise to intriguing collective dynamical phenomena. However, the symmetries of globally and identically coupled identical units do not allow solutions where distinct oscillators are frequency-unlocked—a necessary condition for the emergence of chimeras. Thus, forced symmetry breaking is necessary to observe chimera-type solutions. Here, we consider the bifurcations that arise when full permutational symmetry is broken for the network to consist of coupled populations. We consider the smallest possible network composed of four phase oscillators and elucidate the phase space structure, (partial) integrability for some parameter values, and how the bifurcations away from full symmetry lead to frequency-unlocked weak chimera solutions. Since such solutions wind around a torus they must arise in a global bifurcation scenario. Moreover, periodic weak chimeras undergo a period doubling cascade leading to chaos. The resulting chaotic dynamics with distinct frequencies do not rely on amplitude variation and arise in the smallest networks that support chaos. To summarize, we give an overview of the weak chimera phenomena for two populations of two phase oscillators each.
Despite their simplicity, networks of coupled phase oscillators can give rise to intriguing collective dynamical phenomena. However, the symmetries of globally and identically coupled identical units do not allow solutions where distinct oscillators are frequency-unlocked—a necessary condition for the emergence of chimeras. Thus, forced symmetry breaking is necessary to observe chimera-type solutions. Here, we consider the bifurcations that arise when full permutational symmetry is broken for the network to consist of coupled populations. We consider the smallest possible network composed of four phase oscillators and elucidate the phase space structure, (partial) integrability for some parameter values, and how the bifurcations away from full symmetry lead to frequency-unlocked weak chimera solutions. Since such solutions wind around a torus they must arise in a global bifurcation scenario. Moreover, periodic weak chimeras undergo a period doubling cascade leading to chaos. The resulting chaotic dynamics with distinct frequencies do not rely on amplitude variation and arise in the smallest networks that support chaos. To summarize, we give an overview of the weak chimera phenomena for two populations of two phase oscillators each.
-
H. Hong and Erik A. Martens
First-order like phase transition induced by quenched coupling disorder
Chaos 32:6,063125 (2022); doi:10.1063/5.0078431; arXiv:2111.00893
> Abstract We investigate the collective dynamics of a population of XY model-type oscillators, globally coupled via non-separable interactions that are randomly chosen from a positive or negative value and subject to thermal noise controlled by temperature T. We find that the system at T=0 exhibits a discontinuous, first-order like phase transition from the incoherent to the fully coherent state; when thermal noise is present (T>0), the transition from incoherence to the partial coherence is continuous and the critical threshold is now larger compared to the deterministic case (T=0). We derive an exact formula for the critical transition from incoherent to coherent oscillations for the deterministic and stochastic case based on both stability analysis for finite oscillators as well as for the thermodynamic limit (N→∞) based on a rigorous mean-field theory using graphons, valid for heterogeneous graph structures. Our theoretical results are supported by extensive numerical simulations. Remarkably, the synchronization threshold induced by the type of random coupling considered here is identical to the one found in studies, which consider uniform input or output strengths for each oscillator node [H. Hong and S. H. Strogatz, Phys. Rev. E 84(4), 046202 (2011); Phys. Rev. Lett. 106(5), 054102 (2011)], which suggests that these systems display a "universal" character for the onset of synchronization.
We investigate the collective dynamics of a population of XY model-type oscillators, globally coupled via non-separable interactions that are randomly chosen from a positive or negative value and subject to thermal noise controlled by temperature T. We find that the system at T=0 exhibits a discontinuous, first-order like phase transition from the incoherent to the fully coherent state; when thermal noise is present (T>0), the transition from incoherence to the partial coherence is continuous and the critical threshold is now larger compared to the deterministic case (T=0). We derive an exact formula for the critical transition from incoherent to coherent oscillations for the deterministic and stochastic case based on both stability analysis for finite oscillators as well as for the thermodynamic limit (N→∞) based on a rigorous mean-field theory using graphons, valid for heterogeneous graph structures. Our theoretical results are supported by extensive numerical simulations. Remarkably, the synchronization threshold induced by the type of random coupling considered here is identical to the one found in studies, which consider uniform input or output strengths for each oscillator node [H. Hong and S. H. Strogatz, Phys. Rev. E 84(4), 046202 (2011); Phys. Rev. Lett. 106(5), 054102 (2011)], which suggests that these systems display a "universal" character for the onset of synchronization.
-
H. Hong and Erik A. Martens
A Two-Frequency-Two Coupling model of coupled oscillators
Chaos 31, 083124 (2021); doi:10.1063/5.0056844; arXiv:2107.07897
> Abstract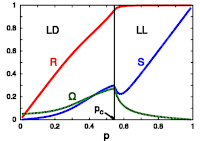 We considered the phase coherence dynamics in a Two-Frequency and Two-Coupling (TFTC) model of coupled oscillators, where coupling strength and natural oscillator frequencies for individual oscillators may assume one of two values (positive/negative). The bimodal distributions for the coupling strengths and frequencies are either correlated or uncorrelated. To study how correlation affects phase coherence, we analyzed the TFTC model by means of numerical simulation and exact dimensional reduction methods allowing to study the collective dynamics in terms of local order parameters. The competition resulting from distributed coupling strengths and natural frequencies produces nontrivial dynamic states. For correlated disorder in frequencies and coupling strengths, we found that the entire oscillator population splits into two subpopulations, both phase-locked (Lock-Lock), or one phase-locked and the other drifting (Lock-Drift), where the mean-fields of the subpopulations maintain a constant non-zero phase difference. For uncorrelated disorder, we found that the oscillator population may split into four phase-locked subpopulations, forming phase-locked pairs, which are either mutually frequency-locked (Stable Lock-Lock-Lock-Lock) or drifting (Breathing Lock-Lock-Lock-Lock), thus resulting in a periodic motion of the global synchronization level. Finally, we found for both types of disorder that a state of Incoherence exists; however, for correlated coupling strengths and frequencies, Incoherence is always unstable, whereas it is only neutrally stable for the uncorrelated case. Numerical simulations performed on the model show good agreement with the analytic predictions. The simplicity of the model promises that real-world systems can be found which display the dynamics induced by such correlated/uncorrelated disorder.
We considered the phase coherence dynamics in a Two-Frequency and Two-Coupling (TFTC) model of coupled oscillators, where coupling strength and natural oscillator frequencies for individual oscillators may assume one of two values (positive/negative). The bimodal distributions for the coupling strengths and frequencies are either correlated or uncorrelated. To study how correlation affects phase coherence, we analyzed the TFTC model by means of numerical simulation and exact dimensional reduction methods allowing to study the collective dynamics in terms of local order parameters. The competition resulting from distributed coupling strengths and natural frequencies produces nontrivial dynamic states. For correlated disorder in frequencies and coupling strengths, we found that the entire oscillator population splits into two subpopulations, both phase-locked (Lock-Lock), or one phase-locked and the other drifting (Lock-Drift), where the mean-fields of the subpopulations maintain a constant non-zero phase difference. For uncorrelated disorder, we found that the oscillator population may split into four phase-locked subpopulations, forming phase-locked pairs, which are either mutually frequency-locked (Stable Lock-Lock-Lock-Lock) or drifting (Breathing Lock-Lock-Lock-Lock), thus resulting in a periodic motion of the global synchronization level. Finally, we found for both types of disorder that a state of Incoherence exists; however, for correlated coupling strengths and frequencies, Incoherence is always unstable, whereas it is only neutrally stable for the uncorrelated case. Numerical simulations performed on the model show good agreement with the analytic predictions. The simplicity of the model promises that real-world systems can be found which display the dynamics induced by such correlated/uncorrelated disorder.
-
T. Du, H. Mestre, B. T. Kress, G. Liu, A. M. Sweeney, A. J. Samson, M. Kaag Rasmussen, K. Nygaard Mortensen, P. A. R. Bork, W. Peng, Genaro E. Olveda, L. Bashford, E. R. Toro, J. Tithof, D. H. Kelley, J. Thomas, P. G. Hjorth, E. A. Martens, R. I. Mehta, H. Hirase, Y. Mori, M. Nedergaard
Cerebrospinal fluid is a significant fluid source for anoxic cerebral edema
Brain, awab293 (2021); doi:10.1093/brain/awab293;
> Abstract Cerebral edema develops after anoxic brain injury. In two models of asphyxial and asystolic cardiac arrest without resuscitation, we found that edema develops shortly after anoxia secondary to terminal depolarizations and the abnormal entry of cerebrospinal fluid (CSF). Edema severity correlated with the availability of CSF with the age-dependent increase in CSF volume worsening the severity of edema. Edema was identified primarily in brain regions bordering CSF compartments in mice and humans. The degree of ex vivo tissue swelling was predicted by an osmotic model suggesting that anoxic brain tissue possesses a high intrinsic osmotic potential. This osmotic process was temperature-dependent, proposing an additional mechanism for the beneficial effect of therapeutic hypothermia. These observations show that CSF is a primary source of edema fluid in anoxic brain. This novel insight offers a mechanistic basis for the future development of alternative strategies to prevent cerebral edema formation after cardiac arrest.
Cerebral edema develops after anoxic brain injury. In two models of asphyxial and asystolic cardiac arrest without resuscitation, we found that edema develops shortly after anoxia secondary to terminal depolarizations and the abnormal entry of cerebrospinal fluid (CSF). Edema severity correlated with the availability of CSF with the age-dependent increase in CSF volume worsening the severity of edema. Edema was identified primarily in brain regions bordering CSF compartments in mice and humans. The degree of ex vivo tissue swelling was predicted by an osmotic model suggesting that anoxic brain tissue possesses a high intrinsic osmotic potential. This osmotic process was temperature-dependent, proposing an additional mechanism for the beneficial effect of therapeutic hypothermia. These observations show that CSF is a primary source of edema fluid in anoxic brain. This novel insight offers a mechanistic basis for the future development of alternative strategies to prevent cerebral edema formation after cardiac arrest.
-
Benjamin Jüttner, Christian Henriksen and Erik A. Martens
Birth and Destruction of Collective Oscillations in a Network of Two Populations of Type 1 Neurons
Chaos 31:2 (2021); doi:10.1063/5.0031630; arXiv:2009.11589
> Abstract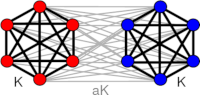 We study the macroscopic dynamics of large networks of excitable type 1 neurons composed of two populations interacting with disparate but symmetric intra- and inter-population coupling strengths. This nonuniform coupling scheme facilitates symmetric equilibria, where both populations display identical firing activity, characterized by either quiescent or spiking behavior, or asymmetric equilibria, where the firing activity of one population exhibits quiescent but the other exhibits spiking behavior. Oscillations in the firing rate are possible if neurons emit pulses with non-zero width but are otherwise quenched. Here, we explore how collective oscillations emerge for two statistically identical neuron populations in the limit of an infinite number of neurons. A detailed analysis reveals how collective oscillations are born and destroyed in various bifurcation scenarios and how they are organized around higher codimension bifurcation points. Since both symmetric and asymmetric equilibria display bistable behavior, a large configuration space with steady and oscillatory behavior is available. Switching between configurations of neural activity is relevant in functional processes such as working memory and the onset of collective oscillations in motor control.
We study the macroscopic dynamics of large networks of excitable type 1 neurons composed of two populations interacting with disparate but symmetric intra- and inter-population coupling strengths. This nonuniform coupling scheme facilitates symmetric equilibria, where both populations display identical firing activity, characterized by either quiescent or spiking behavior, or asymmetric equilibria, where the firing activity of one population exhibits quiescent but the other exhibits spiking behavior. Oscillations in the firing rate are possible if neurons emit pulses with non-zero width but are otherwise quenched. Here, we explore how collective oscillations emerge for two statistically identical neuron populations in the limit of an infinite number of neurons. A detailed analysis reveals how collective oscillations are born and destroyed in various bifurcation scenarios and how they are organized around higher codimension bifurcation points. Since both symmetric and asymmetric equilibria display bistable behavior, a large configuration space with steady and oscillatory behavior is available. Switching between configurations of neural activity is relevant in functional processes such as working memory and the onset of collective oscillations in motor control.
-
Dumitru Călugăru, Jan Frederik Totz, Erik A. Martens and Harald Engel
First-order Synchronization Transition in a Large Population of Strongly Coupled Relaxation Oscillators
Science Advances, 6(39):eabb2637 (2020), doi:10.1126/sciadv.abb2637; arXiv:1812.04727
> Abstract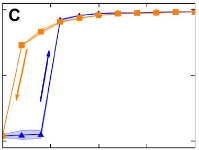 Onset and loss of synchronization in coupled oscillators are of fundamental importance in understanding emergent behavior in natural and man-made systems, which range from neural networks to power grids. We report on experiments with hundreds of strongly coupled photochemical relaxation oscillators that exhibit a discontinuous synchronization transition with hysteresis, as opposed to the paradigmatic continuous transition expected from the widely used weak coupling theory. The resulting first-order transition is robust with respect to changes in network connectivity and natural frequency distribution. This allows us to identify the relaxation character of the oscillators as the essential parameter that determines the nature of the synchronization transition. We further support this hypothesis by revealing the mechanism of the transition, which cannot be accounted for by standard phase reduction techniques.
Onset and loss of synchronization in coupled oscillators are of fundamental importance in understanding emergent behavior in natural and man-made systems, which range from neural networks to power grids. We report on experiments with hundreds of strongly coupled photochemical relaxation oscillators that exhibit a discontinuous synchronization transition with hysteresis, as opposed to the paradigmatic continuous transition expected from the widely used weak coupling theory. The resulting first-order transition is robust with respect to changes in network connectivity and natural frequency distribution. This allows us to identify the relaxation character of the oscillators as the essential parameter that determines the nature of the synchronization transition. We further support this hypothesis by revealing the mechanism of the transition, which cannot be accounted for by standard phase reduction techniques.
-
Marius Yamakou, Poul G. Hjorth and Erik A. Martens
Optimal self-induced stochastic resonance in multiplex neural networks: electrical versus chemical synapses
Frontiers in Computational Neuroscience, 14:62 (2020); doi:10.3389/fncom.2020.00062; arXiv:2002.12443
> Abstract Electrical and chemical synapses shape the dynamics of neural networks, and their functional roles in information processing have been a longstanding question in neurobiology. In this paper, we investigate the role of synapses on the optimization of the phenomenon of self-induced stochastic resonance in a delayed multiplex neural network by using analytical and numerical methods. We consider a two-layer multiplex network in which, at the intra-layer
level, neurons are coupled either by electrical synapses or by inhibitory chemical synapses. For each isolated layer, computations indicate that weaker electrical and chemical synaptic couplings are better optimizers of self-induced stochastic resonance. In addition, regardless of the synaptic strengths, shorter electrical synaptic delays are found to be better optimizers
of the phenomenon than shorter chemical synaptic delays, while longer chemical synaptic delays are better optimizers than longer electrical synaptic delays; in both cases, the poorer optimizers are, in fact, worst. It is found that electrical, inhibitory, or excitatory chemical multiplexing of the two layers having only electrical synapses at the intra-layer levels can
each optimize the phenomenon. Additionally, only excitatory chemical multiplexing of the two layers having only inhibitory chemical synapses at the intra-layer levels can optimize the phenomenon. These results may guide experiments aimed at establishing or confirming to the mechanism of self-induced stochastic resonance in networks of artificial neural circuits as well as in real biological neural networks.
Electrical and chemical synapses shape the dynamics of neural networks, and their functional roles in information processing have been a longstanding question in neurobiology. In this paper, we investigate the role of synapses on the optimization of the phenomenon of self-induced stochastic resonance in a delayed multiplex neural network by using analytical and numerical methods. We consider a two-layer multiplex network in which, at the intra-layer
level, neurons are coupled either by electrical synapses or by inhibitory chemical synapses. For each isolated layer, computations indicate that weaker electrical and chemical synaptic couplings are better optimizers of self-induced stochastic resonance. In addition, regardless of the synaptic strengths, shorter electrical synaptic delays are found to be better optimizers
of the phenomenon than shorter chemical synaptic delays, while longer chemical synaptic delays are better optimizers than longer electrical synaptic delays; in both cases, the poorer optimizers are, in fact, worst. It is found that electrical, inhibitory, or excitatory chemical multiplexing of the two layers having only electrical synapses at the intra-layer levels can
each optimize the phenomenon. Additionally, only excitatory chemical multiplexing of the two layers having only inhibitory chemical synapses at the intra-layer levels can optimize the phenomenon. These results may guide experiments aimed at establishing or confirming to the mechanism of self-induced stochastic resonance in networks of artificial neural circuits as well as in real biological neural networks.
-
Christian Bick, Carlo Laing, Marc Goodfellow and Erik A. Martens
Understanding Synchrony Patterns in Biological and Neural Oscillator Networks through Mean-Field Reductions: A Review
Journal of Mathematical Neuroscience, 10(9) (2020); doi:10.1186/s13408-020-00086-9; arXiv:1902.05307
> Abstract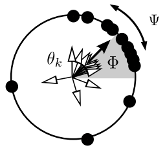 Many biological and neural systems can be seen as networks of interacting periodic processes. Importantly, their functionality, i.e., whether these networks can perform their
function or not, depends on the emerging collective dynamics of the network. Synchrony of oscillations is one of the most prominent examples of such collective behavior and has been
associated both with function and dysfunction. Understanding how network structure and interactions, as well as the microscopic properties of individual units, shape the emerging
collective dynamics is critical to find factors that lead to malfunction. However, many biological systems such as the brain consist of a large number of dynamical units. Hence,
their analysis has either relied on simplified heuristic models on a coarse scale, or the analysis comes at a huge computational cost. Here we review recently introduced approaches,
known as the Ott–Antonsen and Watanabe–Strogatz reductions, allowing one to simplify the analysis by bridging small and large scales. Thus, reduced model equations are
obtained that exactly describe the collective dynamics for each subpopulation in the oscillator network via few collective variables only. The resulting equations are next-generation
models: Rather than being heuristic, they exactly link microscopic and macroscopic descriptions and therefore accurately capture microscopic properties of the underlying system. At
the same time, they are sufficiently simple to analyze without great computational effort. In the last decade, these reduction methods have become instrumental in understanding how
network structure and interactions shape the collective dynamics and the emergence of synchrony. We review this progress based on concrete examples and outline possible limitations.
Finally, we discuss how linking the reduced models with experimental data can guide the way towards the development of new treatment approaches, for example, for neurological
disease.
Many biological and neural systems can be seen as networks of interacting periodic processes. Importantly, their functionality, i.e., whether these networks can perform their
function or not, depends on the emerging collective dynamics of the network. Synchrony of oscillations is one of the most prominent examples of such collective behavior and has been
associated both with function and dysfunction. Understanding how network structure and interactions, as well as the microscopic properties of individual units, shape the emerging
collective dynamics is critical to find factors that lead to malfunction. However, many biological systems such as the brain consist of a large number of dynamical units. Hence,
their analysis has either relied on simplified heuristic models on a coarse scale, or the analysis comes at a huge computational cost. Here we review recently introduced approaches,
known as the Ott–Antonsen and Watanabe–Strogatz reductions, allowing one to simplify the analysis by bridging small and large scales. Thus, reduced model equations are
obtained that exactly describe the collective dynamics for each subpopulation in the oscillator network via few collective variables only. The resulting equations are next-generation
models: Rather than being heuristic, they exactly link microscopic and macroscopic descriptions and therefore accurately capture microscopic properties of the underlying system. At
the same time, they are sufficiently simple to analyze without great computational effort. In the last decade, these reduction methods have become instrumental in understanding how
network structure and interactions shape the collective dynamics and the emergence of synchrony. We review this progress based on concrete examples and outline possible limitations.
Finally, we discuss how linking the reduced models with experimental data can guide the way towards the development of new treatment approaches, for example, for neurological
disease.
-
H. Mestre, T. Du, A. M. Sweeney, G. Liu, A. J. Samson, W. Peng, K. Nygaard Mortensen, F. F. Stæger, P. A. R. Bork, L. Bashford, E. R. Toro, J. Tithof, D. H. Kelley, P. G. Hjorth, Erik A. Martens, R. I. Mehta, O. Solis, P. Blinder, D. Kleinfeld, H. Hirase, Y. Mori, M. Nedergaard
Cerebrospinal fluid influx drives acute ischemic tissue swelling
Science, Research Article, 367(6483):eaax7171 (2020); doi:10.1126/science.aax7171;
> Abstract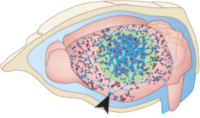 Stroke affects millions each year. Post-stroke brain edema predicts the severity of eventual stroke damage, yet our concept of how edema develops is incomplete and treatment options remain limited. In early stages, fluid accumulation occurs owing to a net gain of ions, widely thought to enter from the vascular compartment. Here we used magnetic resonance imaging, radiolabeled tracers, and multiphoton imaging in rodents, to show instead that cerebrospinal fluid surrounding the brain enters the tissue within minutes of an ischemic insult along perivascular flow channels. This process was initiated by ischemic spreading depolarizations along with subsequent vasoconstriction, which in turn enlarged the perivascular spaces and doubled glymphatic inflow speeds. Thus, our understanding of post-stroke edema needs to be revised and these findings could provide a conceptual basis for development of alternative treatment strategies.
Stroke affects millions each year. Post-stroke brain edema predicts the severity of eventual stroke damage, yet our concept of how edema develops is incomplete and treatment options remain limited. In early stages, fluid accumulation occurs owing to a net gain of ions, widely thought to enter from the vascular compartment. Here we used magnetic resonance imaging, radiolabeled tracers, and multiphoton imaging in rodents, to show instead that cerebrospinal fluid surrounding the brain enters the tissue within minutes of an ischemic insult along perivascular flow channels. This process was initiated by ischemic spreading depolarizations along with subsequent vasoconstriction, which in turn enlarged the perivascular spaces and doubled glymphatic inflow speeds. Thus, our understanding of post-stroke edema needs to be revised and these findings could provide a conceptual basis for development of alternative treatment strategies.
-
Nicolás Deschle, Andreas Daffertshofer, Demian Battaglia and Erik A. Martens
Directed Flow of Information in Chimera States
Frontiers in Applied Mathematics and Statistics, 5, 28, (2019); doi:10.3389/fams.2019.00028; arXiv:1904.11553
> Abstract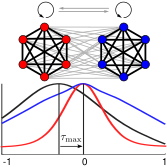 We investigated interactions within chimera states in a phase oscillator network with two coupled subpopulations. To quantify interactions within and between these subpopulations, we estimated the corresponding (delayed) mutual information that — in general— quantifies the capacity or the maximum rate at which information can be transferred to recover a sender's information at the receiver with a vanishingly low error probability. After verifying their equivalence with estimates based on the continuous phase data, we determined the mutual information using the time points at which the individual phases passed through their respective Poincaré sections. This stroboscopic view on the dynamics may resemble, e.g., neural spike times, that are common observables in the study of neuronal information transfer. This discretization also increased processing speed significantly, rendering it particularly suitable for a fine-grained analysis of the effects of experimental and model parameters. In our model, the delayed mutual information within each subpopulation peaked at zero delay, whereas between the subpopulations it was always maximal at non-zero delay, irrespective of parameter choices. We observed that the delayed mutual information of the desynchronized subpopulation preceded the synchronized subpopulation. Put differently, the oscillators of the desynchronized subpopulation were “driving” the ones in the synchronized subpopulation. These findings were also observed when estimating mutual information of the full phase trajectories. We can thus conclude that the delayed mutual information of discrete time points allows for inferring a functional directed flow of information between subpopulations of coupled phase oscillators.
We investigated interactions within chimera states in a phase oscillator network with two coupled subpopulations. To quantify interactions within and between these subpopulations, we estimated the corresponding (delayed) mutual information that — in general— quantifies the capacity or the maximum rate at which information can be transferred to recover a sender's information at the receiver with a vanishingly low error probability. After verifying their equivalence with estimates based on the continuous phase data, we determined the mutual information using the time points at which the individual phases passed through their respective Poincaré sections. This stroboscopic view on the dynamics may resemble, e.g., neural spike times, that are common observables in the study of neuronal information transfer. This discretization also increased processing speed significantly, rendering it particularly suitable for a fine-grained analysis of the effects of experimental and model parameters. In our model, the delayed mutual information within each subpopulation peaked at zero delay, whereas between the subpopulations it was always maximal at non-zero delay, irrespective of parameter choices. We observed that the delayed mutual information of the desynchronized subpopulation preceded the synchronized subpopulation. Put differently, the oscillators of the desynchronized subpopulation were “driving” the ones in the synchronized subpopulation. These findings were also observed when estimating mutual information of the full phase trajectories. We can thus conclude that the delayed mutual information of discrete time points allows for inferring a functional directed flow of information between subpopulations of coupled phase oscillators.
-
Erik A. Martens and Konstantin Klemm
Cyclic Structure Induced by Load Fluctuations in Adaptive Transportation Networks
ECMI book subseries of Mathematics in Industry (2019); doi:10.1007/978-3-030-27550-19; arXiv:1810.10049
> Abstract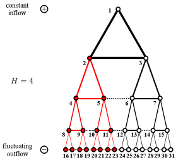 Transport networks are crucial to the functioning of natural systems and technological infrastructures. For flow networks in many scenarios, such as rivers or blood vessels, acyclic networks (i.e., trees) are optimal structures when assuming time-independent in- and outflow. Dropping this assumption, fluctuations of net flow at source and/or sink nodes may render the pure tree solutions unstable even under a simple local adaptation rule for conductances. Here, we consider tree-like networks under the influence of spatially heterogeneous distribution of fluctuations, where the root of the tree is supplied by a constant source and the leaves at the bottom are equipped with sinks with fluctuating loads. We find that the network divides into two regions characterized by tree-like motifs and stable cycles. The cycles emerge through transcritical bifurcations at a critical amplitude of fluctuation. For a simple network structure, depending on parameters defining the local adaptation, cycles first appear close to the leaves (or root) and then appear closer towards the root (or the leaves). The interaction between topology and dynamics gives rise to complex feedback mechanisms with many open questions in the theory of network dynamics. A general understanding of the dynamics in adaptive transport networks is essential in the study of mammalian vasculature, and adaptive transport networks may find technological applications in self-organizing piping systems.
Transport networks are crucial to the functioning of natural systems and technological infrastructures. For flow networks in many scenarios, such as rivers or blood vessels, acyclic networks (i.e., trees) are optimal structures when assuming time-independent in- and outflow. Dropping this assumption, fluctuations of net flow at source and/or sink nodes may render the pure tree solutions unstable even under a simple local adaptation rule for conductances. Here, we consider tree-like networks under the influence of spatially heterogeneous distribution of fluctuations, where the root of the tree is supplied by a constant source and the leaves at the bottom are equipped with sinks with fluctuating loads. We find that the network divides into two regions characterized by tree-like motifs and stable cycles. The cycles emerge through transcritical bifurcations at a critical amplitude of fluctuation. For a simple network structure, depending on parameters defining the local adaptation, cycles first appear close to the leaves (or root) and then appear closer towards the root (or the leaves). The interaction between topology and dynamics gives rise to complex feedback mechanisms with many open questions in the theory of network dynamics. A general understanding of the dynamics in adaptive transport networks is essential in the study of mammalian vasculature, and adaptive transport networks may find technological applications in self-organizing piping systems.
-
Christian Bick, Mark J. Panaggio and Erik A. Martens
Chaos in Kuramoto Oscillator Networks
Chaos (AIP), 28, 071102 (2018), Fast Track; doi:10.1063/1.5041444; arXiv:1802.05481
EDITOR's PICK
> Abstract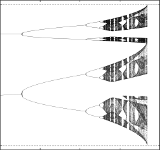
Kuramoto oscillators are widely used to explain collective phenomena in networks of coupled oscillatory units. We show that simple networks of two populations with a generic coupling scheme can exhibit chaotic dynamics as conjectured by Ott and Antonsen [Chaos, 18, 037113 (2008)]. These chaotic mean field dynamics arise universally across network size, from the continuum limit of infinitely many oscillators down to very small networks with just two oscillators per population. Hence, complicated dynamics are expected even in the simplest description of oscillator networks.
-
Erik A. Martens and Konstantin Klemm
Transitions from Trees to Cycles in Adaptive Flow Networks
Frontiers in Physics, Vol. 5, Article 62, 2017, Open Access; arXiv:1711.00401
Supplementary Videos here.
> Abstract
Transport networks are crucial to the functioning of natural and technological systems. Nature features transport networks that are adaptive over a vast range of parameters, thus providing an impressive level of robustness in supply. Theoretical and experimental studies have found that real-world transport networks exhibit both tree-like motifs and cycles. When the network is subject to load fluctuations, the presence of cyclic motifs may help to reduce flow fluctuations and, thus, render supply in the network more robust. While previous studies considered network topology via optimization principles, here, we take a dynamical systems approach and study a simple model of a flow network with dynamically adapting weights (conductances). We assume a spatially non-uniform distribution of rapidly fluctuating loads in the sinks and investigate what network configurations are dynamically stable. The network converges to a spatially non-uniform stable configuration composed of both cyclic and tree-like structures. Cyclic structures emerge locally in a transcritical bifurcation as the amplitude of the load fluctuations is increased. The resulting adaptive dynamics thus partitions the network into two distinct regions with cyclic and tree-like structures. The location of the boundary between these two regions is determined by the amplitude of the fluctuations. These findings may explain why natural transport networks display cyclic structures in the micro-vascular regions near terminal nodes, but tree-like features in the regions with larger veins.
-
Erik A. Martens, Christian Bick and Mark J. Panaggio
Chimera States in Two Populations with Heterogeneous Phase-lag
Chaos 26 (9), 094819 (2016); doi:10.1063/1.4958930; arXiv:1606.0187
> Abstract
The simplest network of coupled phase-oscillators exhibiting chimera states is given by two populations with disparate intra- and inter-population coupling strengths. We explore the effects of heterogeneous coupling phase-lags between the two populations. Such heterogeneity arises naturally in various settings, for example as an approximation to transmission delays, excitatory-inhibitory interactions, or as amplitude and phase responses of oscillators with electrical or mechanical coupling. We find that breaking the phase-lag symmetry results in a variety of states with uniform and non-uniform synchronization, including in-phase and anti-phase synchrony, full incoherence (splay state), chimera states with phase separation of 0 or π between populations, and states where both populations remain desynchronized. These desynchronized states exhibit stable, oscillatory, and even chaotic dynamics. Moreover, we identify the bifurcations through which chimera and desynchronized states emerge. Stable chimera states and desynchronized solutions, which do not arise for homogeneous phase-lag parameters, emerge as a result of competition between synchronized in-phase, anti-phase equilibria, and fully incoherent states when the phase-lags are near ±π/2 (cosine coupling). These findings elucidate previous experimental results involving a network of mechanical oscillators and provide further insight into the breakdown of synchrony in biological systems.
-
D.D. Postnov, D. J. Marsh, D. E. Postnov, T.H. Braunstein, N.H. Holstein-Rathlou, Erik A. Martens, and O. Sosnovtseva.
Modeling of Kidney Hemodynamics: Probability-Based Topology of an Arterial Network.
PLoS Computational Biology 12(7): e1004922 (2016). doi:10.1371/journal.pcbi.1004922
> Abstract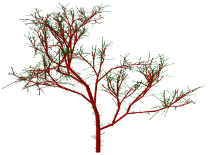
Through regulation of the extracellular fluid volume, the kidneys provide important long-term regulation of blood pressure. At the level of the individual functional unit (the nephron), pressure and flow control involves two different mechanisms that both produce oscillations. The nephrons are arranged in a complex branching structure that delivers blood to each nephron and, at the same time, provides a basis for an interaction between adjacent nephrons. The functional consequences of this interaction are not understood, and at present it is not possible to address this question experimentally. We provide experimental data and a new modeling approach to clarify this problem. To resolve details of microvascular structure, we collected 3D data from more than 150 afferent arterioles in an optically cleared rat kidney. Using these results together with published micro-computed tomography (μCT) data we develop an algorithm for generating the renal arterial network. We then introduce a mathematical model describing blood flow dynamics and nephron to nephron interaction in the network. The model includes an implementation of electrical signal propagation along a vascular wall. Simulation results show that the renal arterial architecture plays an important role in maintaining adequate pressure levels and the self-sustained dynamics of nephrons.
-
Erik A. Martens, Mark Panaggio, Daniel M. Abrams
Basins of Attraction for Chimera States
New Journal of Physics, Fast Track Communication, 18:022002 (2016), Open Access; doi:10.1088/1367-2630/18/2/022002; arXiv:1507.01457
Supplementary Videos here.
> Abstract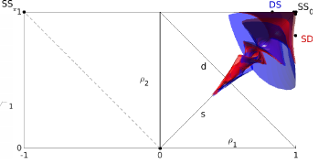
Chimera states---curious symmetry-broken states in systems of identical coupled oscillators---typically occur only for certain initial conditions. Here we analyze their basins of attraction in a simple system comprised of two populations. Using perturbative analysis and numerical simulation we evaluate asymptotic states and associated destination maps, and demonstrate that basins form a complex twisting structure in phase space. Understanding the basins' precise nature may help in the development of control methods to switch between chimera patterns, with possible technological and neural system applications.
-
Simona Olmi, Erik A. Martens, Shashi Thutupalli, Alessandro Torcini
Intermittent Chaotic Chimeras for Coupled Rotators
Phys. Rev. E Rapid Communications, 92, 030901 (R) (2015), doi:10.1103/PhysRevE.92.030901; arXiv:1507.07685
>Abstract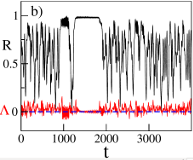
Two symmetrically coupled populations of N oscillators with inertia m display chaotic solutions with broken symmetry similar to experimental observations with mechanical pendula. In particular, we report the first evidence of intermittent chaotic chimeras, where one population is synchronized and the other jumps erratically between laminar and turbulent phases. These states have finite life-times diverging as a power-law with N and m. Lyapunov analyses reveal chaotic properties in quantitative agreement with theoretical predictions for globally coupled dissipative systems.
-
Erik A. Martens*, Navish Wadhwa*, Nis S. Jacobsen, Christian Lindemann, Ken H. Andersen, and André Visser
Size Structures Sensory Hierarchy in Ocean Life
Proceedings of the Royal Society B, 282:20151346 (2015); doi:10.1101/018937; biorXiv:10.1101/018937
>AbstractSupplementary Text (Press Release)
Life in the ocean is shaped by the trade-off between a need to encounter other organisms for feeding or mating, and to avoid encounters with predators. Avoiding or achieving encounters necessitates an efficient means of collecting the maximum possible information from the surroundings through the use of remote sensing. In this study, we explore how sensing mode and range depend on body size. We reveal a hierarchy of sensing modes (chemosensing, mechanosensing, vision, hearing, and echolocation) where body size determines the available battery of sensing modes and where larger body size means a longer sensing range. The size-dependent hierarchy and the transitions between primary sensory modes are explained on the grounds of limiting factors set by physiology and the physical laws governing signal generation, transmission and reception. We characterize the governing mechanisms and theoretically predict the body size limits for various sensory modes, which align very well with size ranges found in literature. The treatise of all ocean life, from unicellular organisms to whales, demonstrates how body size determines available sensing modes, and thereby acts as a major structuring factor of aquatic life.
-
K.H. Andersen, T. Berge, R.J. Gonçalves, M. Hartvig, J. Heuschele, S. Hylander,
N.S. Jacobsen, C.Lindemann, E.A. Martens, A.B. Neuheimer, K. Olsson, A. Palacz,
F. Prowe, J.Sainmont, S.J. Traving, A.W. Visser, N. Wadhwa and T. Kiørboe
Characteristic Sizes of Life in the Oceans, from Bacteria to Whales.
Annual Review of Marine Science, 8:3.1–3.25 (2016); doi:10.1146/annurev-marine-122414-034144
>Abstract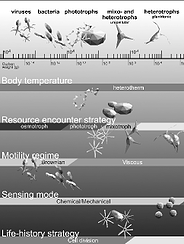
The size of an individual organism is a key trait to characterize its physiology and feeding ecology. Size-based scaling laws may have a limited size range of validity or undergo a transition from one scaling exponent to another at some characteristic size. We collate and review data on size-based scaling laws for resource acquisition, mobility, sensory range, and progeny size for all pelagic marine life, from bacteria to whales. Further, we review and develop simple theoretical arguments for observed scaling laws and the characteristic sizes of a change or breakdown of power laws. We divide life in the ocean into seven major realms based on trophic strategy, physiology, and life history strategy. Such a categorization represents a move away from a taxonomically oriented description toward a trait-based description of life in the oceans. Finally, we discuss life forms that transgress the simple size-based rules and identify unanswered questions.
-
Christian Bick and Erik A. Martens
Controlling Chimeras
New Journal of Physics 17:033030 (2015), Open Access; doi:10.1088/1367-2630/17/3/033030; arXiv:1402.6363
Supplementary Video here.
>Abstract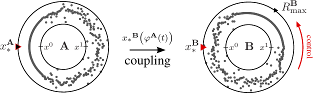 Coupled phase oscillators model a variety of dynamical phenomena in nature and technological applications. Non-local coupling gives rise to chimera states which are characterized by a distinct part of phase-synchronized oscillators while the remaining ones move incoherently. Here, we apply the idea of control to chimera states: using gradient dynamics to exploit drift of a chimera, it will attain any desired target position. Through control, chimera states become functionally relevant; for example, the controlled position of localized synchrony may encode information and perform computations. Since functional aspects are crucial in (neuro-)biology and technology, the localized synchronization of a chimera state becomes accessible to develop novel applications. Based on gradient dynamics, our control strategy applies to any suitable observable and can be generalized to arbitrary dimensions. Thus, the applicability of chimera control goes beyond chimera states in non-locally coupled systems.
Coupled phase oscillators model a variety of dynamical phenomena in nature and technological applications. Non-local coupling gives rise to chimera states which are characterized by a distinct part of phase-synchronized oscillators while the remaining ones move incoherently. Here, we apply the idea of control to chimera states: using gradient dynamics to exploit drift of a chimera, it will attain any desired target position. Through control, chimera states become functionally relevant; for example, the controlled position of localized synchrony may encode information and perform computations. Since functional aspects are crucial in (neuro-)biology and technology, the localized synchronization of a chimera state becomes accessible to develop novel applications. Based on gradient dynamics, our control strategy applies to any suitable observable and can be generalized to arbitrary dimensions. Thus, the applicability of chimera control goes beyond chimera states in non-locally coupled systems.
-
C. Kuehn*, Erik A. Martens*, D. Romero
Critical Transitions in Social Network Activity
Journal of Complex Networks 2(2), p.1-12 (2014); doi:10.1093/comnet/cnt022; arXiv:1307.8250
> AbstractCovered in Oxford University Press Blog, 2014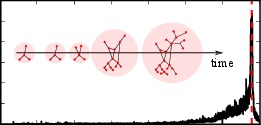 A large variety of complex systems in ecology, climate science, biomedicine and engineering have been observed to exhibit tipping points, where the dynamical state of the system abruptly changes. For example, such critical transitions may result in the sudden change of ecological environments and climate conditions. Data and models suggest that detectable warning signs may precede some of these drastic events. This view is also corroborated by abstract mathematical theory for generic bifurcations in stochastic multi-scale systems. Whether such stochastic scaling laws used as warning signs for apriori unknown events in society are present in social networks is an exciting open problem, to which at present only highly speculative answers can be given. Here, we instead provide a first step towards tackling a simpler question by focusing on a priori known events and analyse a social media data set with a focus on classical variance and autocorrelation warning signs. Our results thus pertain to one absolutely fundamental question: Can the stochastic warning signs known from other areas also be detected in large-scale social media data? We answer this question affirmatively as we find that several apriori known events are preceded by variance and autocorrelation growth. Our findings thus clearly establish the necessary starting point to further investigate the relationship between abstract mathematical theory and various classes of critical transitions in social networks.
A large variety of complex systems in ecology, climate science, biomedicine and engineering have been observed to exhibit tipping points, where the dynamical state of the system abruptly changes. For example, such critical transitions may result in the sudden change of ecological environments and climate conditions. Data and models suggest that detectable warning signs may precede some of these drastic events. This view is also corroborated by abstract mathematical theory for generic bifurcations in stochastic multi-scale systems. Whether such stochastic scaling laws used as warning signs for apriori unknown events in society are present in social networks is an exciting open problem, to which at present only highly speculative answers can be given. Here, we instead provide a first step towards tackling a simpler question by focusing on a priori known events and analyse a social media data set with a focus on classical variance and autocorrelation warning signs. Our results thus pertain to one absolutely fundamental question: Can the stochastic warning signs known from other areas also be detected in large-scale social media data? We answer this question affirmatively as we find that several apriori known events are preceded by variance and autocorrelation growth. Our findings thus clearly establish the necessary starting point to further investigate the relationship between abstract mathematical theory and various classes of critical transitions in social networks.
-
Erik A. Martens, Shashi Thutupalli, Antoine Fourrière and Oskar Hallatschek
Chimera States in Mechanical Oscillator Networks
Proc. Natl. Acad. Sci., Vol. 110 (26), p. 10563–10567 (2013); doi:10.1073/pnas.1302880110; arXiv:1301.7608
Supplementary informations here and here.
>AbstractFeatured in Physik Journal, "Die Schimäre lebt", by Arkady Pikovsky, Michael Rosenblum and Jürgen Kurths. Issue of September 2013.
 The synchronization of coupled oscillators is a striking manifestation of self-organization that nature employs to orchestrate essential processes of life, such as the beating of the heart. While it was long thought that synchrony or disorder were mutually exclusive steady states for a network of identical oscillators, numerous theoretical studies over the last 10 years revealed the intriguing possibility of `chimera states', in which the symmetry of the oscillator population is broken into a synchronous and an asynchronous part. Particularly, numerous analytical studies, involving different network topologies, and various sources of random perturbations establish chimeras as a robust theoretical concept and suggest that they exist in complex systems in nature. Yet, a striking lack of empirical evidence raises the question of whether chimeras are indeed characteristic to natural systems. This calls for a palpable realization of chimera states without any fine-tuning, from which physical mechanisms underlying their emergence can be uncovered. Here, we devise a simple experiment with mechanical oscillators coupled in a hierarchical network to show that chimeras emerge naturally from a competition between two antagonistic synchronization patterns. We identify a wide spectrum of complex states, encompassing and extending the set of previously described chimeras. Our mathematical model shows that the self-organization observed in our experiments is controlled by elementary dynamical equations from mechanics that are ubiquitous in many natural and technological systems. The symmetry breaking mechanism revealed by our experiments may thus be prevalent in systems exhibiting collective behaviour, such as power grids, opto-mechanical crystals or cells communicating via quorum sensing in microbial populations.
The synchronization of coupled oscillators is a striking manifestation of self-organization that nature employs to orchestrate essential processes of life, such as the beating of the heart. While it was long thought that synchrony or disorder were mutually exclusive steady states for a network of identical oscillators, numerous theoretical studies over the last 10 years revealed the intriguing possibility of `chimera states', in which the symmetry of the oscillator population is broken into a synchronous and an asynchronous part. Particularly, numerous analytical studies, involving different network topologies, and various sources of random perturbations establish chimeras as a robust theoretical concept and suggest that they exist in complex systems in nature. Yet, a striking lack of empirical evidence raises the question of whether chimeras are indeed characteristic to natural systems. This calls for a palpable realization of chimera states without any fine-tuning, from which physical mechanisms underlying their emergence can be uncovered. Here, we devise a simple experiment with mechanical oscillators coupled in a hierarchical network to show that chimeras emerge naturally from a competition between two antagonistic synchronization patterns. We identify a wide spectrum of complex states, encompassing and extending the set of previously described chimeras. Our mathematical model shows that the self-organization observed in our experiments is controlled by elementary dynamical equations from mechanics that are ubiquitous in many natural and technological systems. The symmetry breaking mechanism revealed by our experiments may thus be prevalent in systems exhibiting collective behaviour, such as power grids, opto-mechanical crystals or cells communicating via quorum sensing in microbial populations.
Appeared in Physics Today, Backscatter: "A Mechanical Chimera". Vol. 66, Issue 10 of October 2013.
FOKOS award for the most surprising/striking discovery reported in 2013 (PDF of Award)
-
Erik A. Martens, S. Watanabe and T. Bohr
Model for Polygonal Hydraulic Jumps
Phys. Rev. E, Vol. 85, 036316 (2012); doi:10.1103/PhysRevE.85.036316; arXiv:1111.4599
Supplementary Videos here
>Abstract
We propose a phenomenological model for the polygonal hydraulic jumps discovered by Ellegaard and co-workers [Nature (London) 392, 767 (1998); Nonlinearity 12, 1 (1999); Physica B 228, 1 (1996)], based on the known flow structure for the type-II hydraulic jumps with a “roller” (separation eddy) near the free surface in the jump region. The model consists of mass conservation and radial force balance between hydrostatic pressure and viscous stresses on the roller surface. In addition, we consider the azimuthal force balance, primarily between pressure and viscosity, but also including nonhydrostatic pressure contributions from surface tension in light of recent observations by Bush and co-workers [J. Fluid Mech. 558, 33 (2006); Phys. Fluids 16, S4 (2004)]. The model can be analyzed by linearization around the circular state, resulting in a parameter relationship for nearly circular polygonal states. A truncated but fully nonlinear version of the model can be solved analytically. This simpler model gives rise to polygonal shapes that are very similar to those observed in experiments, even though surface tension is neglected, and the condition for the existence of a polygon with N corners depends only on a single dimensionless number φ. Finally, we include time-dependent terms in the model and study linear stability of the circular state. Instability occurs for sufficiently small Bond number and the most unstable wavelength is expected to be roughly proportional to the width of the roller as in the Rayleigh-Plateau instability.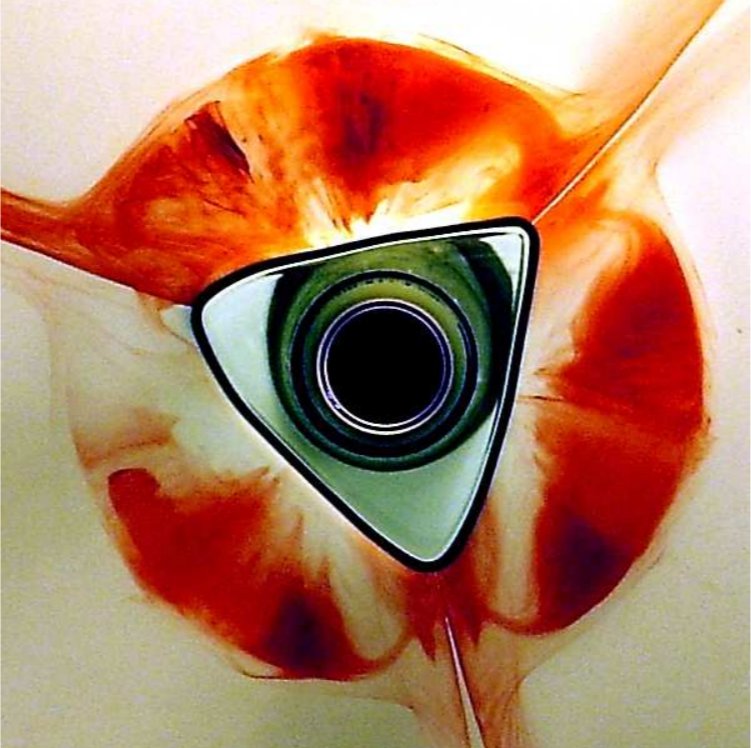
Highlighted in Physical Review E. Kaleidoscope
> Read Summary Text
-
Erik A. Martens, R. Kostadinov, C. C. Maley and O. Hallatschek
Spatial Structure Increases the Waiting for Cancer
New Journal of Physics 13, 115014 (2011); doi:10.1088/1367-2630/13/11/115014; arXiv:1106.3005
Focus Issue "Physics of Cancer"
>Abstract
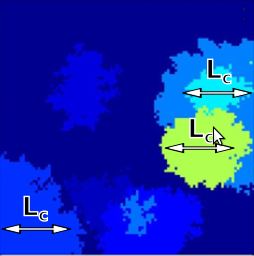 Cancer results from a sequence of genetic and epigenetic changes that lead to a variety of abnormal phenotypes including increased proliferation and survival of somatic cells and thus to a selective advantage of pre-cancerous cells. The notion of cancer progression as an evolutionary process has been attracting increasing interest in recent years. A great deal of effort has been made to better understand and predict the progression to cancer using mathematical models; these mostly consider the evolution of a well-mixed cell population, even though pre-cancerous cells often evolve in highly structured epithelial tissues. In this study, we propose a novel model of cancer progression that considers a spatially structured cell population where clones expand via adaptive waves. This model is used to assess two different paradigms of asexual evolution that have been suggested to delineate the process of cancer progression. The standard scenario of periodic selection assumes that driver mutations are accumulated strictly sequentially over time. However, when the mutation supply is sufficiently high, clones may arise simultaneously on distinct genetic backgrounds, and clonal adaptation waves interfere with each other. We find that in the presence of clonal interference, spatial structure increases the waiting time for cancer, leads to a patchwork structure of non-uniformly sized clones and decreases the survival probability of virtually neutral (passenger) mutations, and that genetic distance begins to increase over a characteristic length scale Lc. These characteristic features of clonal interference may help us to predict the onset of cancers with pronounced spatial structure and to interpret spatially sampled genetic data obtained from biopsies. Our estimates suggest that clonal interference likely occurs in the progression of colon cancer and possibly other cancers where spatial structure matters.
Cancer results from a sequence of genetic and epigenetic changes that lead to a variety of abnormal phenotypes including increased proliferation and survival of somatic cells and thus to a selective advantage of pre-cancerous cells. The notion of cancer progression as an evolutionary process has been attracting increasing interest in recent years. A great deal of effort has been made to better understand and predict the progression to cancer using mathematical models; these mostly consider the evolution of a well-mixed cell population, even though pre-cancerous cells often evolve in highly structured epithelial tissues. In this study, we propose a novel model of cancer progression that considers a spatially structured cell population where clones expand via adaptive waves. This model is used to assess two different paradigms of asexual evolution that have been suggested to delineate the process of cancer progression. The standard scenario of periodic selection assumes that driver mutations are accumulated strictly sequentially over time. However, when the mutation supply is sufficiently high, clones may arise simultaneously on distinct genetic backgrounds, and clonal adaptation waves interfere with each other. We find that in the presence of clonal interference, spatial structure increases the waiting time for cancer, leads to a patchwork structure of non-uniformly sized clones and decreases the survival probability of virtually neutral (passenger) mutations, and that genetic distance begins to increase over a characteristic length scale Lc. These characteristic features of clonal interference may help us to predict the onset of cancers with pronounced spatial structure and to interpret spatially sampled genetic data obtained from biopsies. Our estimates suggest that clonal interference likely occurs in the progression of colon cancer and possibly other cancers where spatial structure matters.
Reviewed in 'Cancer in Light of Experimental Evolution' by Sprouffske, Merlo, Gerrish, Maley, Sniegowski. Current Biology 22, (2012).
-
Erik A. Martens and O. Hallatschek
Interfering Waves of Adaptation Promote Spatial Mixing
Genetics 189(3), 1045–1060 (2011), Open Access; doi:10.1534/genetics.111.130112
>Abstract
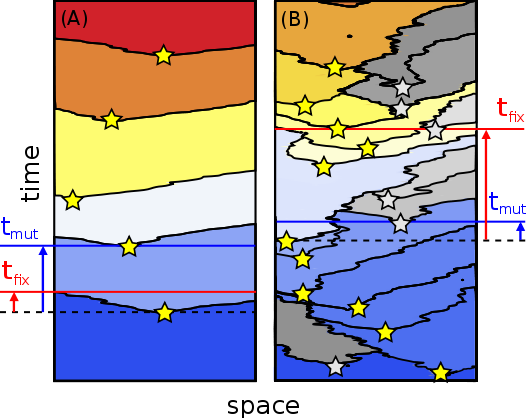
A fundamental problem of asexual adaptation is that beneficial substitutions are not efficiently accumulated in large populations: Beneficial mutations often go extinct because they compete with one another in going to fixation. It has been argued that such clonal interference may have led to the evolution of sex and recombination in well-mixed populations. Here, we study clonal interference, and mechanisms of its mitigation, in an evolutionary model of spatially structured populations with uniform selection pressure. Clonal interference is much more prevalent with spatial structure than without, due to the slow wave-like spread of beneficial mutations through space. We find that the adaptation speed of asexuals saturates when the linear habitat size exceeds a characteristic interference length, which becomes shorter with smaller migration and larger mutation rate. The limiting speed is proportional to μ1/2 and μ1/3 in linear and planar habitats, respectively, where the mutational supply μ is the product of mutation rate and local population density. This scaling and the existence of a speed limit should be amenable to experimental tests as they fall far below predicted adaptation speeds for well-mixed populations (that scale as the logarithm of population size). Finally, we show that not only recombination, but also long-range migration is a highly efficient mechanism of relaxing clonal competition in structured populations. Our conservative estimates of the interference length predict prevalent clonal interference in microbial colonies and biofilms, so clonal competition should be a strong driver of both genetic and spatial mixing in those contexts.
Highlighted in ’Cutting through the complexity of cell collectives’ by Nadell, Bucci, Drescher, Levin, Bassler, Xavier. Proc. R. Soc. B, 280 (2013).
-
Erik A. Martens
Chimeras in a Network of Three Oscillator Populations with Varying Network Topology
Chaos 20, 043122 (2010); doi:10.1063/1.3499502; arXiv:1003.2916
>Abstract
 We study a network of three populations of coupled phase oscillators with identical frequencies. The populations interact nonlocally, in the sense that all oscillators are coupled to one another, but more weakly to those in neighboring populations than to those in their own population. Using this system as a model system, we discuss for the first time the influence of network topology on the existence of so-called chimera states. In this context, the network with three populations represents an interesting case because the populations may either be connected as a triangle, or as a chain, thereby representing the simplest discrete network of either a ring or a line segment of oscillator populations. We introduce a special parameter that allows us to study the effect of breaking the triangular network structure, and to vary the network symmetry continuously such that it becomes more and more chain-like. By showing that chimera states only exist for a bounded set of parameter values, we demonstrate that their existence depends strongly on the underlying network structures, and conclude that chimeras exist on networks with a chain-like character.
We study a network of three populations of coupled phase oscillators with identical frequencies. The populations interact nonlocally, in the sense that all oscillators are coupled to one another, but more weakly to those in neighboring populations than to those in their own population. Using this system as a model system, we discuss for the first time the influence of network topology on the existence of so-called chimera states. In this context, the network with three populations represents an interesting case because the populations may either be connected as a triangle, or as a chain, thereby representing the simplest discrete network of either a ring or a line segment of oscillator populations. We introduce a special parameter that allows us to study the effect of breaking the triangular network structure, and to vary the network symmetry continuously such that it becomes more and more chain-like. By showing that chimera states only exist for a bounded set of parameter values, we demonstrate that their existence depends strongly on the underlying network structures, and conclude that chimeras exist on networks with a chain-like character.
-
Erik A. Martens
Bistable Chimeras on a Triangular Network of Oscillator Populations
Phys. Rev. E, Vol. 82, 016216 (2010); doi:10.1103/PhysRevE.82.016216; arXiv:1003.2827
>Abstract
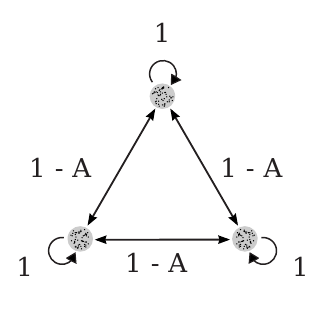 We study a triangular network of three populations of coupled phase oscillators with identical frequencies. The populations interact nonlocally, in the sense that all oscillators are coupled to one another, but more weakly to those in neighboring populations than to those in their own population. This triangular network is the simplest discretization of a continuous ring of oscillators. Yet it displays an unexpectedly different behavior: in contrast to the lone stable chimera observed in continuous rings of oscillators, we find that this system exhibits two coexisting stable chimeras. Both chimeras are, as usual, born through a saddle-node bifurcation. As the coupling becomes increasingly local in nature they lose stability through a Hopf bifurcation, giving rise to breathing chimeras, which in turn get destroyed through a homoclinic bifurcation. Remarkably, one of the chimeras reemerges by a reversal of this scenario as we further increase the locality of the coupling, until it is annihilated through
another saddle-node bifurcation.
We study a triangular network of three populations of coupled phase oscillators with identical frequencies. The populations interact nonlocally, in the sense that all oscillators are coupled to one another, but more weakly to those in neighboring populations than to those in their own population. This triangular network is the simplest discretization of a continuous ring of oscillators. Yet it displays an unexpectedly different behavior: in contrast to the lone stable chimera observed in continuous rings of oscillators, we find that this system exhibits two coexisting stable chimeras. Both chimeras are, as usual, born through a saddle-node bifurcation. As the coupling becomes increasingly local in nature they lose stability through a Hopf bifurcation, giving rise to breathing chimeras, which in turn get destroyed through a homoclinic bifurcation. Remarkably, one of the chimeras reemerges by a reversal of this scenario as we further increase the locality of the coupling, until it is annihilated through
another saddle-node bifurcation.
-
Erik A. Martens, C. R. Laing and S. H. Strogatz
Solvable Model of a Spiral Wave Chimeras
Phys. Rev. Lett., Vol. 104, 044101 (2010); doi:10.1103/PhysRevLett.104.044101; arXiv:0910.5389
>Abstract
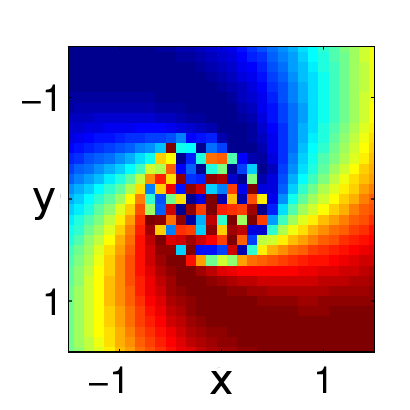
Spiral waves are ubiquitous in two-dimensional systems of chemical or biological oscillators coupled locally by diffusion. At the center of such spirals is a phase singularity, a topological defect where the oscillator amplitude drops to zero. But if the coupling is nonlocal, a new kind of spiral can occur, with a circular core consisting of desynchronized oscillators running at full amplitude. Here, we provide the first analytical description of such a spiral wave chimera and use perturbation theory to calculate its rotation speed and the size of its incoherent core.
Featured in A. Motter, Spontaneous synchrony breaking, News and Views, Nature Physics 6 (2010)
-
Erik A. Martens, E. Barreto, S. H. Strogatz, E. Ott, P. So and T. Antonsen
Exact Results for the Kuramoto Model with a Bimodal Frequency Distribution
Phys. Rev. E, Vol. 79, No.2 (2009); doi:10.1103/PhysRevE.79.026204; arXiv:0809.2129
>Abstract
 We analyze a large system of globally coupled phase oscillators whose natural frequencies are bimodally distributed. The dynamics of this system has been the subject of long-standing interest. In 1984 Kuramoto proposed several conjectures about its behavior; ten years later, Crawford obtained the first analytical results by means of a local center manifold calculation. Nevertheless, many questions have remained open, especially about the possibility of global bifurcations. Here we derive the system’s stability diagram for the special case where the bimodal distribution consists of two equally weighted Lorentzians. Using an ansatz recently discovered by Ott and Antonsen, we show that in this case the infinite-dimensional problem reduces exactly to a flow in four dimensions. Depending on the parameters and initial conditions, the long-term dynamics evolves to one of three states: incoherence, where all the oscillators are desynchronized; partial synchrony, where a macroscopic group of phase-locked oscillators coexists with a sea of desynchronized ones; and a standing wave state, where two counter-rotating groups of phase-locked oscillators emerge. Analytical results are presented for the bifurcation boundaries between these states. Similar results are also obtained for the case in which the bimodal distribution is given by the sum of two Gaussians.
We analyze a large system of globally coupled phase oscillators whose natural frequencies are bimodally distributed. The dynamics of this system has been the subject of long-standing interest. In 1984 Kuramoto proposed several conjectures about its behavior; ten years later, Crawford obtained the first analytical results by means of a local center manifold calculation. Nevertheless, many questions have remained open, especially about the possibility of global bifurcations. Here we derive the system’s stability diagram for the special case where the bimodal distribution consists of two equally weighted Lorentzians. Using an ansatz recently discovered by Ott and Antonsen, we show that in this case the infinite-dimensional problem reduces exactly to a flow in four dimensions. Depending on the parameters and initial conditions, the long-term dynamics evolves to one of three states: incoherence, where all the oscillators are desynchronized; partial synchrony, where a macroscopic group of phase-locked oscillators coexists with a sea of desynchronized ones; and a standing wave state, where two counter-rotating groups of phase-locked oscillators emerge. Analytical results are presented for the bifurcation boundaries between these states. Similar results are also obtained for the case in which the bimodal distribution is given by the sum of two Gaussians.
Other publications
-
Erik A. Martens and S. Thutupalli
Backscatter: A Mechanical Chimera
Physics Today, 66, 10, 92, (2013); doi:10.1063/PT.3.2159;
> Abstract The counterintuitive, complex synchronization state known as a chimera was discovered theoretically a decade ago: In an ensemble of coupled oscillators, two incongruous domains, one synchronized and one desynchronized, can coexist even when the oscillators are identical and the system is symmetric. Chimera states made their laboratory debut last year in a pair of experiments - one with optical oscillators, another with chemical oscillators, both exploiting computer-mediated feedback (see PHYSICS TODAY, October 2012, page 17). Now, with just springs, swings, and metronomes, a quartet of researchers rooted in the Max Planck Institute for Dynamics and Self-Organization in Göttingen, Germany, has achieved the first purely mechanical implementation of chimera states.On the left, 15 metronomes sit on a swing that, through its left-right motion, couples the metronomes to each other. (It was with a similar setup that Christiaan Huygens discovered spontaneous synchronization 300 years ago.) A pair of springs connects the left swing to an identically loaded swing on the right and provides weak coupling between the two metronome sets. Such nonlocal, nonuniform coupling is key for chimeric behavior. When illuminated with UV light, fluorescent spots on the metronome pendulums leave bright blue trails that, for certain spring constants and metronome frequencies, manifest a chimera state: While the metronomes on one swing tick in unison, the other metronomes oscillate incoherently. Since the mechanical elements have ready analogues in numerous physical, biological, and chemical systems, the emergence of complex collective behavior may be relevant in diverse settings, from neural dynamics to power grids. (E. A. Martens et al., Proc. Natl. Acad. Sci. USA 110, 10563, 2013.
The counterintuitive, complex synchronization state known as a chimera was discovered theoretically a decade ago: In an ensemble of coupled oscillators, two incongruous domains, one synchronized and one desynchronized, can coexist even when the oscillators are identical and the system is symmetric. Chimera states made their laboratory debut last year in a pair of experiments - one with optical oscillators, another with chemical oscillators, both exploiting computer-mediated feedback (see PHYSICS TODAY, October 2012, page 17). Now, with just springs, swings, and metronomes, a quartet of researchers rooted in the Max Planck Institute for Dynamics and Self-Organization in Göttingen, Germany, has achieved the first purely mechanical implementation of chimera states.On the left, 15 metronomes sit on a swing that, through its left-right motion, couples the metronomes to each other. (It was with a similar setup that Christiaan Huygens discovered spontaneous synchronization 300 years ago.) A pair of springs connects the left swing to an identically loaded swing on the right and provides weak coupling between the two metronome sets. Such nonlocal, nonuniform coupling is key for chimeric behavior. When illuminated with UV light, fluorescent spots on the metronome pendulums leave bright blue trails that, for certain spring constants and metronome frequencies, manifest a chimera state: While the metronomes on one swing tick in unison, the other metronomes oscillate incoherently. Since the mechanical elements have ready analogues in numerous physical, biological, and chemical systems, the emergence of complex collective behavior may be relevant in diverse settings, from neural dynamics to power grids. (E. A. Martens et al., Proc. Natl. Acad. Sci. USA 110, 10563, 2013.
-
Erik A. Martens
Cooperative Behavior in Networks of Coupled Oscillators
Ph.D. thesis, Cornell University, USA (2009) eCommons@Cornell
>Abstract
 This thesis comprises three problems related to the dynamics of coupled phase oscillators, described by variants of the Kuramoto
model. Kuramoto originally made strong assumptions to simplify the analysis of the oscillator behavior: the phases obey a sinusoidal response curve, their natural frequencies are unimodally distributed, and the oscillators are globally coupled, i.e. all oscillators are coupled with equal strength. Investigating three problems we study what behavior may emerge as we relax the last two of these assumptions. In the first problem, we study the impact of replacing the unimodal with a bimodal frequency distribution on the oscillator dynamics. Based on a recent breakthrough in the field, we are able to determine the complete stability diagram, and determine all types of cooperative behavior that may occur. In the next two problems we break with the assumption of global coupling; a similar simplification that is frequently used is to consider the limit of local, i.e. nearest neighbor
coupling. We investigate what types of new behavior emerge in the intermediate regime that we call nonlocal coupling, and study under which conditions it persists. For nonlocal coupling, a new kind of state has been observed, where synchronized and desynchronized oscillators coexist side by side in a stable fashion. This state is referred to as a chimera state. In the second problem we discuss a triangular network of oscillator populations with nonlocal coupling. For this network topology, we discover that bistable chimera attractors are possible. For the third problem, we study a generalization of this system, and break the ro- tational symmetry inherent to the triangle by introducing an additional parameter. This parameter allows us to change the topology of the network continuously, such that the network attains a more chain-like character; this enables us to study the effect of network topology on the existence of chimera attractors.
This thesis comprises three problems related to the dynamics of coupled phase oscillators, described by variants of the Kuramoto
model. Kuramoto originally made strong assumptions to simplify the analysis of the oscillator behavior: the phases obey a sinusoidal response curve, their natural frequencies are unimodally distributed, and the oscillators are globally coupled, i.e. all oscillators are coupled with equal strength. Investigating three problems we study what behavior may emerge as we relax the last two of these assumptions. In the first problem, we study the impact of replacing the unimodal with a bimodal frequency distribution on the oscillator dynamics. Based on a recent breakthrough in the field, we are able to determine the complete stability diagram, and determine all types of cooperative behavior that may occur. In the next two problems we break with the assumption of global coupling; a similar simplification that is frequently used is to consider the limit of local, i.e. nearest neighbor
coupling. We investigate what types of new behavior emerge in the intermediate regime that we call nonlocal coupling, and study under which conditions it persists. For nonlocal coupling, a new kind of state has been observed, where synchronized and desynchronized oscillators coexist side by side in a stable fashion. This state is referred to as a chimera state. In the second problem we discuss a triangular network of oscillator populations with nonlocal coupling. For this network topology, we discover that bistable chimera attractors are possible. For the third problem, we study a generalization of this system, and break the ro- tational symmetry inherent to the triangle by introducing an additional parameter. This parameter allows us to change the topology of the network continuously, such that the network attains a more chain-like character; this enables us to study the effect of network topology on the existence of chimera attractors.
Talks and Presentations
- Workshop on Dynamics of Evolving Networks, Vrije Universiteit, Amsterdam, NL, July 2023
Invited Talk. Complex dynamics in adaptive networks of phase oscillators. - SIAM Conference on Applications of Dynamical Systems (DS23),
Portland, USA, Minisymposium on "Network Dynamics", May 2023
Invited Talk. Complex dynamics in adaptive networks of phase oscillators. - IMFUFA Seminar.
Roskilde University Center, Denmark, Feb 2023.
Invited Talk. Problems in co-evolutionary network dynamics: theory and applications. - Dynamics Days Europe, , Aberdeen, UK, Sep 21-26, 2022.
Invited Talk. Complex dynamics in adaptive network systems. -
Workshop: Chimera States: From Theory and Experiments to Technology and Living Systems, Max Planck Institute for Complex Systems, Dresden, 2022 (postponed from May 2020 due to COVID-19 outbreak).
Invited Talk. - Bridging the Gap: from Brain Mechanics to Brain Dynamics, Lorentz Center, Netherlands, 25-29 Oct, 2021.
Invited Talk. - Int. Workshop: MRI imaging of the glymphatic/lymphatic system: Emerging topics, University of Copenhagen,
Denmark, Oct 4-6, 2021. (Postponed from 2020 due to COVID-19 outbreak).
Invited Talk. - Dynamics Days Europe, Nice, France,
2021.
Mini-symposium on "Network dynamics with state-dependent interactions and applicatiosn to
biology and medicine", 2021
Invited Talk. - Dynamical Systems Seminar, Courant Institute of Mathematical Sciences, New York, USA, 29 April, 2021.
Invited Talk. - Centre for Mathematical Sciences, Lund University, Sweden, 23 April,
2021.
Invited Talk. - Dynamics Days Digital Europe, 2020. Mini-symposium on "Symmetry breaking in collective behavior: swarming, flocking and chimeras", 2020
Invited Talk. - SIAM Conference on Applications of Dynamical Systems (DS19),
Utah, USA, Minisymposium on "Regular and Chaotic Dynamics of Oscillator Populations in the Kuramoto Model and Beyond", 23 May 2019
Invited Talk. - School and Workshop on Patterns of Synchrony: Chimera States and Beyond | (smr 3286), Abdus Salam International Centre for Theoretical Physics,
Trieste, Italy, May 2019
Invited Lecture. - Dynamics Days Europe, Loughbourough, United Kingdom, Sep 2018
Invited Talk. - The 20th European Conference on Mathematics for Industry, Bolyai Institute, Budapest, Hungary, Jun 2018. Minisymposium on "Multidisciplinary Approaches to Biological Modelling".
Invited talk (minisymposium). - Workshop on Long-range Interactions and Synchronization. International Centre for Theoretical Physics (ICTP-SAIFR), South American Institute for Fundamental Research, Sao Paolo, Brazil, May 2018.
Invited Talk. Video link - IMFUFA Seminar.
Roskilde University Center, Denmark, April 2018.
Invited Talk. Two problems in self-organized network dynamics. - Symposium: Synchronization patterns in networks of nonlinear oscillators,
Berlin Center for Studies of Complex Chemical Systems (BCSCCS), Technische Universität Berlin, Dec 2017.
Invited Talk. - Workshop: Future Trends in Mathematical Biology: In vitro, in vivo, and in silico,
Technical University of Denmark (DTU), Nov 2017.
Invited Talk. - Advanced Study Group "From Microscopic to Collective Dynamics in Neural Circuits",
Max Planck Institute for Complex Systems, Aug 2017.
Invited Talk. - SIAM Applications of Dynamical Systems.
Snowbird, Utah, USA, May 2017.
Talk. -
ICMS Winterschool Complexity. TU Eindhoven, Netherlands, February 2017.
Invited Topical lecture. -
Institute for Cross-Disciplinary Physics and Complex Systems (IFISC), Campus Universitat de les Illes Balears, Palma, Spain, January 2017.
Invited Talk. -
Biomedical Engineering Group. Dept. of Electrical Engineering, Technical University of Denmark (DTU), Kgs. Lyngby, Denmark, January 2017.
Invited Talk. -
International Conference on Control of Complex Systems and Networks. Collaborative Research Center 910 (SFB910), Heringsdorf, Germany, September 2016.
Invited Talk. - Dynamics Days Europe, Corfu, Greece, June 2016
Talk. -
Workshop on synchronization and oscillators with generalized coupling, University of Exeter, United Kingdom, April 2016.
Organizers: Chris Bick, Peter Ashwin, Kyle Wedgwood.
Invited Talk. -
Dynamical Systems Interdisciplinary Network Seminar, Denmark, Oct 2016.
Talk. -
Workshop on Cancer Evolution Through Space And Time (CEST), September 2015, Max-Planck Institute for Evolutionary Biology in Plön, Germany.
Invited Talk: Cancer Progression and Evolution in Spatially Structured Tissues. -
Workshop: Dynamics of Coupled Oscillators: 40 years of the Kuramoto Model, Max Planck Institute for Complex Systems, Dresden, July 2015
Invited Talk: From Kuramoto to Mechanical Chimeras - and Back Again. -
SIAM Applications of Dynamical Systems, Snowbird, May 2015.
Talk: Basins of Attraction for Chimera States. -
DPG Spring meeting, Berlin, Mar 2015.
Invited Talk: Basins of attraction of chimera states. -
"Collective dynamics in coupled oscillator systems", Weierstrass Institute, Berlin, Nov 2014.
Talk: Chimeras, Controlling and basins of attractions. -
Dynamical Systens Interdisciplinary Network Seminar, Denmark, Oct 2014.
Talk: A tale of Greek monsters, the brain, control, and a bit about networks. -
Dynamics Days Europe, Bayreuth, Sep 2014.
Talk: Controlling Chimeras. -
Istituto dei Sistemi Complessi - Consiglio Nazionale delle Ricerche CNR/INFN, Firenze, Italy, Dec 2013.
Invited Talk: Chimera states - mythological monsters from math arise in the real world -
International Conference on Systems Biology, Copenhagen, Sep 2013.
Talk: Spatial structure increases the waiting time for cancer -
Trait-based approaches to Ocean Life (International Workshop), Copenhagen, Aug 2013.
Poster: Trait-based modeling of trophic chains and seasonal forcing -
Complex Motion in Fluids, DTU Summer School, Krogerup, Denmark, Aug 2013.
Poster: Chimera States in Mechanical Oscillator Networks -
Dynamics Days Europe, Madrid, Jun 2013.
Talk: Chimera states - how mythological monsters from math arise in the real world -
SIAM Applications of Dynamical Systems, Snowbird, USA, May 2013.
Talk: Realization of Chimera States in a Network of Mechanical Oscillators -
Department of Engineering Sciences and Applied Mathematics, Northwestern University, Chicago, USA, May 2013.
Invited talk: Chimera states - mythological monsters from mathematics in the real world -
Niels Bohr Institute, Copenhagen, March 2013
Invited Talk: Chimera States - or how mathematical creatures emerge in the real world -
Dept. of Biomedical Sciences, Copenhagen University, Dec 2012
Invited Talk: Chimera States - mythological monsters from mathematics in the real world -
Dynamics Days Europe, Gothenburg, September 2012
Talk: (with Demian Battaglia): Self-organized routing of information in hierarchic networks of oscillators -
Dynamics Days Europe, Gothenburg, September 2012
Talk: Realization of chimeras in a network of mechanical oscillators -
Department of Mathematics, Technical University of Denmark, April 2012
Invited talk: Synchronization and symmetry breaking in coupled oscillators networks -
Centre for congestive diseases (N. Wright),
Blizard Institute of Cell and Molecular Science, Queen Mary, University of London (UK), March 2012
Invited talk: Evolution in Spatially Structured Cell Populations and Cancer Progression -
Institute for Chemistry and Biology of the Marine Environment (ICBM),
Carl von Ossietzky University, Oldenburg (Germany), Februar 2012
Invited talk: Adaptation in Spatially Extended Populations
-
Statistical Physics / Theory of Chaos Group (Arkady Pikovsky), University of Potsdam, Germany, January 2012
Invited talk: Speed of evolution in spatially structured populations and dynamics of interfering Fisher waves
-
Niels Bohr Institute Copenhagen, Københavns Universitet, Copenhagen, January 2012
Invited talk: Problems in oscillator dynamics and in evolutionary dynamics of spatially structured habitats
-
XXXI Dynamics Days Europe, Oldenburg (Germany), September 2011
Talk: Dynamical model of spatial evolution and cancer progression
-
75th Annual Meeting of the DPG and DPG Spring Meeting: Section on Statistical Physics and Biological Evolution, Dresden (Germany), March 2011
Talk: Speed of evolution in spatially extended populations
-
Laboratory of Genetics (de Visser Group), Wageningen University (NL), November 2010
Invited talk: Speed of adaptation in spatially extended populations
-
EMBO Conference Series: Experimental Approaches to Evolution and Ecology using Yeast, EMBL Heidelberg, September 2010
Poster: Speed of evolution in spatially extended populations
-
Annual Meeting of the Society for Molecular Biology and Evolution (SMBE) in Lyon, July 2010
Talk: Speed of adaptation in spatially extended systems
-
Statistical Physics / Theory of Chaos Group (Arkady Pikovsky), University of Potsdam, Germany, January 2010:
Invited talk: Chimera states in 2D nonlocally coupled oscillator systems
- FOR 608 Nonlineary Dynamics, University of Bayreuth, Germany, October 2009:
Talk: Coexistence of synchronized and desynchronized states in nonlocally coupled oscillator systems
- Dynamics Days Europe, Göttingen, August 2009:
Talk: Coexistence of synchronized and desynchronized states in coupled oscillators
- SIAM Conference on Applications of Dynamical Systems, Snowbird, May 17 2009:
Talk: Kuramoto model with bimodal distribution (minisymposium)
-
Fluid Dynamics Group (Paul Steen), Chemical Engineering, Cornell University, Ithaca, November 2008
Invited Talk: Pattern formation in fluids
- Gordon Conference, Nonlinear Science, Maine, 2005:
Poster: Pattern formation in fluids: polygonal hydraulic jumps
- Complex Motions in Fluids, Summer School at Krogerup Højskole, Denmark
Talk: The hydraulic jump and Its polygonal regime